Смещение — это разница между исходным и конечным положением пути, пройденного объектом. Узнайте, как найти смещение с помощью уравнений и его свойств, а также изучите определение и примеры смещения в этом уроке.
Определения и свойства
Вы начинаете из дома, едете в продуктовый магазин, который находится в 20 милях от вас, а затем возвращаетесь домой. Вы преодолели расстояние 40 миль туда и обратно, но ваше перемещение было равно нулю за этот путь туда и обратно. Перемещение и расстояние — это две величины, которые необходимо определить, чтобы каждая величина была полностью понята. Кроме того, мы не можем говорить о смещении, не сравнивая его с расстоянием.
Рассмотрим этот рисунок (см. видео), на котором показаны три разных пути между точками А и В.
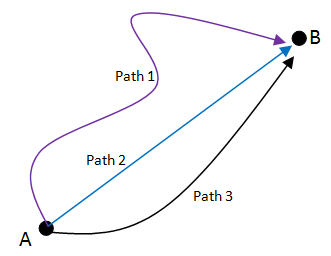
Три пути из пункта А в пункт Б
Путь 1 покрывает наибольшее расстояние, а Путь 2 покрывает наименьшее расстояние. Однако все три пути имеют одинаковое смещение. Это связано с тем, что расстояние относится к фактической длине пути, пройденного объектом. Несмотря на то, что все три пути начинаются и заканчиваются в одном и том же месте, каждый путь проходит на разное расстояние. Расстояние — скалярная величина , поэтому оно всегда является положительным числом, независимо от того, в каком направлении движется объект. Таким образом, для любого пути пройденное расстояние всегда увеличивается.
Смещение , однако, относится к разнице между конечной позицией и начальной позицией пути, по которому движется объект. Итак, на рисунке выше показано, что смещению не важно, что происходит между начальной и конечной точками пути; все, что имеет значение, — это расстояние между начальной и конечной точками пути.
Свойства и уравнение для смещения
Смещение является векторной величиной , а это значит, что нам нужно указать величину и направление. Таким образом, в отличие от расстояния, для смещения важно, в каком направлении движется объект, когда он перемещается между двумя точками. Итак, в одном измерении смещение может быть положительным, отрицательным или нулевым. Помните, смещение зависит от начального и конечного положения пути, пройденного объектом.
Это формула смещения:
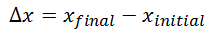
Дельта x (или дельта y ) — это математический символ смещения. Дельта относится к изменению. В данном случае под изменением понимается расстояние между конечным и начальным положениями объекта. Давайте рассмотрим несколько разных примеров и воспользуемся формулой для расчета смещения объектов при их перемещении между точками на пути, чтобы представить все в перспективе.
Примеры смещения
Рассмотрим путь, показанный на этом рисунке. Предположим, что расстояния, отмеченные на рисунке, указаны в метрах.

Конечное положение составляет 5 метров, а начальное положение - 0 метров. Используя формулу, мы можем рассчитать смещение как 5 метров минус 0 метров, что равно 5 метрам. В этом случае пройденное расстояние также составляет 5 метров. Смещение на этом рисунке составляет 5 метров.
Теперь рассмотрим путь, показанный на следующем рисунке.

Конечное положение составляет 0 метров, а начальное положение - 5 метров. Смещение составляет 0 метров минус 5 метров, что дает нам смещение в -5 метров. Смещение в этом случае отрицательное. Расстояние, пройденное в этом примере, по-прежнему составляет 5 метров.
Наконец, рассмотрим путь, показанный на этом последнем рисунке:

Конечное положение равно 0 метрам, а начальное положение равно 0 метрам. Это дает нам смещение в 0 метров. В этом примере пройденное расстояние составляет 10 метров. Это означает, что ваше смещение всегда равно 0 всякий раз, когда вы возвращаетесь туда, откуда начали. Итак, всякий раз, когда вы едете на работу утром и возвращаетесь домой с работы вечером, ваше смещение за день составляет 0 метров.
Краткое содержание урока
Смещение - это векторная величина, поэтому нам нужно указать величину и направление, чтобы полностью охарактеризовать его. В отличие от расстояния, которое может только увеличиваться на любом пройденном пути, смещение может быть положительным, отрицательным или нулевым. Смещение равно нулю, когда вы начинаете и заканчиваете в одном и том же месте. Как мы видели в примерах, расстояние и смещение, пройденные по разным путям, редко бывают точными, потому что расстояние - это скалярная величина, а смещение - векторная величина. Наконец, смещение зависит только от начала и конца; промежуток между ними не имеет значения; перемещение не зависит от пути.