Линейные отношения изображаются в виде прямой линии, тогда как прямые отношения могут быть линейными, но могут включать кривую, поскольку одна переменная изменяется с разной скоростью. Изучите эти две разные концепции и значение интерпретации данного наклона с помощью примеров задач на графиках.
Линейные отношения
Когда ученые работают над экспериментом, они часто собирают большие наборы данных. Чтобы понять, что означают все числа в этих наборах данных, полезно найти способ их визуализации. Чаще всего ученые делают это с помощью графиков. С помощью графика мы можем посмотреть на два набора чисел, образующих наши точки данных, и попытаться выяснить взаимосвязь между ними.
Одно из самых простых отношений, которое мы можем увидеть на графике, — это линейное отношение. В линейной зависимости точки данных образуют прямую линию наилучшего соответствия. Мы называем линию, созданную из точек данных графика, кривой, даже если она прямая. Для линейной зависимости мы можем представить кривую математически, используя форму уравнения линии с пересечением наклона :
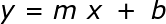
Мы называем это формой пересечения наклона, потому что здесь m — наклон, а b — пересечение y. Наклон дает нам меру крутизны кривой, а точка пересечения y указывает нам точку, в которой кривая проходит через ось y графика. Последние две переменные, x и y , являются координатами любой точки на кривой.
Давайте рассмотрим пример линейной зависимости, с которой вы можете столкнуться в курсе естественных наук. Вам когда-нибудь приходилось переводить температуру из градусов Цельсия в градусы Фаренгейта? Если да, то для этого вы использовали следующую формулу:
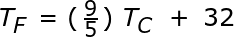
Если мы посмотрим на наше уравнение линии, приведенное ранее, мы увидим, что это уравнение преобразования имеет точно такую же форму, где 9/5 — это наклон, а 32 — точка пересечения по оси y . Когда мы наносим на график диапазон температур по Фаренгейту и по Цельсию, мы видим, что он действительно образует линейную зависимость.
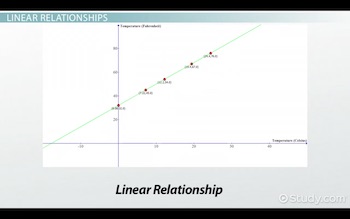
Фаренгейты против Цельсия
Прямые отношения
В прямой зависимости при увеличении одной переменной увеличивается другая или при уменьшении одной уменьшается другая. Часто вы будете сталкиваться с особой формой прямой зависимости, называемой прямо пропорциональной зависимостью, в которой переменные увеличиваются или уменьшаются с одинаковой скоростью, а кривая проходит через начало координат (0,0) на графике. Это особая форма линейной зависимости, которая дает нам y -пересечение нуля, изменяя наше уравнение линии на следующее:
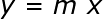
В прямо пропорциональных отношениях наш наклон является константой, то есть это число, которое никогда не меняется. Для прямо пропорционального отношения мы называем это константой пропорциональности .
В вводном курсе физики вы обнаружите, что прямо пропорциональные отношения проявляются довольно часто. Известным примером этого является 2-й закон Ньютона:
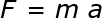
Здесь сила ( F ) и ускорение ( a ) прямо пропорциональны друг другу, пока масса объекта ( m ) не меняется.
Интерпретация наклона
Как в линейных, так и в прямых отношениях наклон был важной концепцией, но что он означает? Мы уже говорили в общем, что наклон — это мера крутизны кривой графика, но давайте немного конкретнее. Уклон определяется как подъем над пробегом. Подъем — это изменение по вертикали между двумя точками на линии, а прогон — это изменение по горизонтали между двумя точками на линии. Математически мы можем записать это следующим образом:
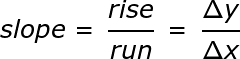
Давайте представим, как, например, будет выглядеть наклон 1/2 на нашем графике. Это означало бы, что на каждую единицу, которую мы перемещаем по вертикали на графике, мы перемещаемся по горизонтали на 2 единицы.
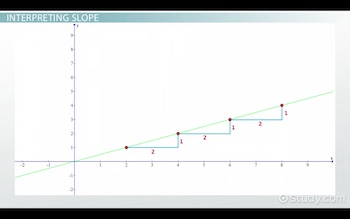
Наклон 1/2