Когда на объект действует несколько сил, сложение векторов вычисляет общую силу, действующую на объект.
Зачем нам нужно добавлять векторы
Напрмиер, вы находитесь на ярмарке и принимаете участие в перетягивании каната с участием нескольких команд. В центре находится кольцо с пятью привязанными к нему веревками, а на конце каждой веревки находится команда для перетягивания каната. Как только начинается война, все пять команд борются изо всех сил. Одни тянут с большими усилиями, другие с меньшими усилиями. Но в каком направлении движется кольцо? В какую сторону ускоряется?
Чтобы найти ответ на этот вопрос, нам нужно найти общую сумму векторов сил каждой из команд. Если две команды тянут в противоположных направлениях с одинаковой силой, они уравновешиваются, но с учетом количества сил, которые могут быть задействованы в реальных ситуациях, невозможно сказать, какой будет общая сила. Чтобы вычислить общую силу, мы должны сложить векторы сил.
То же самое может произойти и с другими видами векторов. Если вы идете в движущемся поезде, в то время как Земля движется вокруг Солнца, а Солнце вращается вокруг центра галактики, ваше тело имеет множество различных векторов скорости. Если вы хотите узнать свою общую скорость, вам придется их сложить.
Существует два основных способа сложения векторов: математический и геометрический. В этом уроке мы рассмотрим геометрический подход: сложение векторов от кончика к хвосту.
Геометрический подход
Чтобы избежать большого количества запутанной математики, геометрический подход отличается простотой. Все, что вам нужно сделать, это нарисовать схему. Конечно, вам нужно нарисовать очень точную схему — чертеж в масштабе . Чертеж в масштабе — это чертеж, на котором длины и углы каждой линии соотносятся друг с другом согласованным образом, соответствующим действительности. Так, например, с вектором силы можно сказать, что каждый сантиметр равен силе в 10 ньютонов. Таким образом, вектор силы в 50 ньютонов будет стрелой длиной 5 сантиметров.
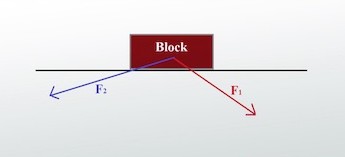
Первая диаграмма
Чтобы получить сумму двух векторов, вы рисуете их в масштабе и прикладываете хвост (обратную сторону стрелки) одного вектора к кончику (точке) другого вектора. Если, например, у нас есть два вектора силы, толкающие блок, один человек толкает блок вниз и вправо, а другой — вниз и влево. Мы перемещаем один из этих векторов на конец другого.
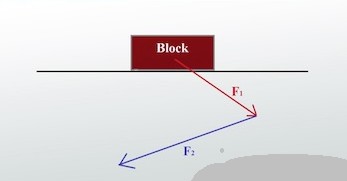
Вторая диаграмма
И если эту диаграмму масштабировать, мы можем найти сумму, нарисовав вектор и стрелку от самого начала до самого конца. Этот вектор, который мы нарисовали, является суммой. Вектор силы 1 плюс вектор силы 2 равняется общей силе. Затем мы могли бы измерить длину стрелки на нашем чертеже в масштабе и угол, под которым указывает стрелка, чтобы вычислить некоторые числа для нашей общей силы.
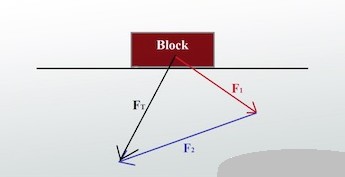
Окончательная схема
Пример
Возможно, было бы проще, если бы мы рассмотрели пример. Вернемся к перетягиванию каната с 5 участниками, но для удобства сделаем 3 команды. Вот масштабный рисунок сил на кольце в центре:
И вопрос просит нас найти полную силу, используя геометрические подходы. Ну, все, что нам нужно сделать, это сложить три вектора силы от кончика к хвосту. Переместите это сюда, а это сюда (см. видео на 03:03). Затем нарисуйте вектор от начала до конца:
И это наша последняя сила, наша общая сила, которая говорит нам, что кольцо будет ускоряться в этом направлении.
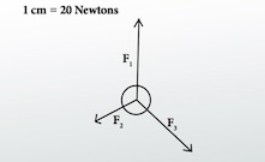
Измеряем стрелку, и она оказывается длиной 3 сантиметра, что по шкале составляет 60 ньютонов. А угол, под которым на него направлена эта сила, равен 25 градусам. Таким образом, общая сила, действующая на кольцо, составляет 60 ньютонов под углом 25 градусов, отсчитываемым от положительной оси x. Вот и все; это наш окончательный ответ.
Резюме урока
В реальном мире часто в одной ситуации действует множество векторов. Множество сил, действующих на один и тот же объект, множество скоростей, множество электрических полей… все это примеры векторов. Чтобы вычислить чистый результат действия всех этих сил (или скоростей, или полей), особенно когда они направлены во всевозможных противоположных направлениях, мы должны вычислить общее количество. Мы делаем это, складывая векторы вместе.
Мы можем складывать векторы математически или геометрически. Чтобы сделать это геометрически, мы должны создать чертеж в масштабе. Затем мы берем векторы, которые хотим добавить, и перемещаем их так, чтобы они располагались от кончика к хвосту. Если мы нарисуем вектор от самого начала до самого конца, это будет наша сумма. Его длина будет размером суммы, а его направление будет направлением суммы. Пока все нарисовано в масштабе, как по длине, так и по направлению, мы можем просто измерить нашу окончательную стрелку и получить ответ. И это все, что нужно для геометрического сложения векторов.