Изучите три закона движения планет Кеплера. Узнайте, как работа Кеплера с Тихо Браге помогла в формулировании этих законов.
Есть три закона, которые управляют тем, как планеты в нашей Солнечной системе вращаются вокруг Солнца. Эти три закона были сформулированы немецким астрономом по имени Иоганн Кеплер, который опубликовал их между 1609 и 1619 годами.
В начале пятнадцатого века астрономы мира знали, что Солнце является центром Солнечной системы. Они в основном верили в теории, выдвинутые Николаем Коперником в 1540-х годах, которые утверждают, что все планеты движутся вокруг Солнца по идеально круглым орбитам.

Иоганн Кеплер
Около 1600 года Кеплер начал работать с датским астрономом по имени Тихо Браге. Браге построил новую астрономическую обсерваторию в Праге, где вел невероятно подробные и точные наблюдения за движением планет и звезд по ночному небу. Используя три закона движения планет Кеплера, Кеплер начал замечать некоторые расхождения в наблюдаемом положении планеты Марс, по сравнению с ее предсказанным положением по модели Коперника.
Кеплер искал причину этого несоответствия, которое в конечном итоге привело его к разработке этих трех законов движения планет.

Тихо Браге
Три закона Кеплера
1-й закон Кеплера
- Орбита планеты вокруг Солнца представляет собой эллипс, с Солнцем в одном фокусе.
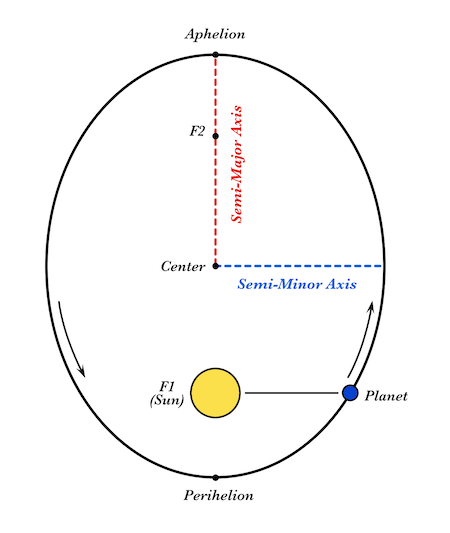
Первый закон движения планет гласит, что орбиты планет эллиптические, а не круговые.
Вопреки популярному научному мнению того времени, что орбиты планет были идеально круглыми, Кеплер обнаружил, что орбиты на самом деле эллиптические. Эллипс похож на овал или уплощенный круг.
Круг имеет центр — расстояние от любой точки вдоль края до центра окружности всегда одинаково. Эллипс, с другой стороны, имеет два фокуса (множественное число фокуса). Для любой точки вдоль края эллипса сумма расстояний до двух фокусов всегда постоянна.
Величина удлинения эллипса называется эксцентриситетом, который описывает, как далеко друг от друга находятся очаги. Эксцентриситет эллипса может находиться в любом месте от 0 до 1. Эллипс с эксцентриситетом 0 означает, что его фокусы не имеют расстояния между ними, другими словами, окружности. Эксцентриситет 1 подразумевает, что фокусы бесконечно далеки друг от друга — это описывает форму, которая больше не является эллипсом, а параболой или плоской кривой с открытым концом. Эксцентриситет орбиты Земли составляет 0,017, что очень близко к кругу. Орбита Меркурия составляет 0,205, что делает его самой эксцентричной орбитой любой планеты в Солнечной системе.
Размер круга можно измерить по его диаметру: расстоянию от одной стороны круга, через центр, до другой стороны. Радиус окружности вдвое меньше: расстояние от центра окружности до края. Поскольку он «сплющен» по сравнению с окружностью, ни диаметр, ни радиус не могут быть определены для эллипса. Вместо этого расстояние через «короткую» сторону эллипса определяется как малая ось, а расстояние через «длинную» сторону определяется как большая ось. Половина малой оси (от центра до короткой стороны) называется полумощной осью, а половина большой оси называется большой полуосью.
При определении размеров планетарных орбит астрономы обычно ссылаются на большую полуось планеты. Большая полуось орбиты Земли составляет около 150 миллионов км (93 миллиона миль).
Первый закон Кеплера также гласит, что Солнце находится в одном фокусе эллиптической орбиты планеты, а не в самом центре. Это означает, что по мере того, как планета движется по своей орбите, она будет периодически перемещаться все ближе и дальше от Солнца. Точка на орбите планеты, которая находится ближе всего к Солнцу, называется перигелием. Точка, которая находится дальше всего, называется афелием.
Земля обычно достигает афелия около 5 июля каждого года. Перигелий происходит около 5 января каждого года. Там Земля находится примерно на 5 миллионов км (3 миллиона миль) ближе к Солнцу в перигелии, чем в афелии. Это может показаться несколько отсталым для людей, живущих в Северном полушарии Земли, потому что зима — самое холодное время года — на самом деле происходит, когда Земля находится ближе всего к Солнцу. Эта разница в расстоянии на самом деле не оказывает существенного влияния на сезоны Земли — ежегодное изменение сезонов в основном связано с наклоном земной оси на 23,5 °.
2-й закон Кеплера
Воображаемая линия, соединяющая планету с Солнцем, будет выметать равные области в течение равных периодов времени.
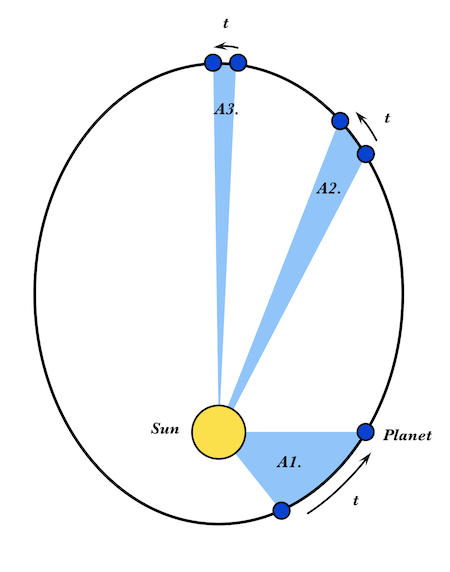
Второй закон движения планет гласит, что объекты движутся быстрее по своим орбитам, когда они находятся ближе к Солнцу.
Партнерство с Тихо Браге
Кеплер отправил копию своей книги не кому иному, как Галилею и Тихо Браге, датскому астроному. Тихо был, вероятно, самым известным астрономом своего времени. Поэтому, когда Тихо пригласил Кеплера стать его помощником в Праге в 1600 году, вы можете поверить, что Кеплер с готовностью согласился. В следующем году Тихо умер, и Кеплер стал имперским математиком.
Благодаря тщательным наблюдениям Тихо за движением планет, Кеплер начал изучать и наблюдать за движением Марса и, используя свои исключительные математические способности, к 1606 году выяснил истинную орбитальную природу Марса. вытянутый эллипс. Такое открытие полностью развеяло 2000-летнюю веру в то, что планеты движутся по кругу.
Кеплер также обнаружил, что планеты не движутся с одинаковой скоростью по всему эллипсу. Вместо этого они двигаются быстрее, когда находятся ближе к солнцу. Его результаты были опубликованы в книге под названием Astronomia Nova (Новая астрономия).
Прежде чем мы перейдем к законам движения планет Кеплера, которые я как бы уже рассказал, я хочу определить, что такое эллипс, чтобы вы могли немного лучше понять один из законов Кеплера.
Эллипс — это кривая, окружающая две точки, называемые фокусами, так что общее расстояние от одного фокуса до точки на эллипсе и обратно до другого фокуса постоянно для каждой точки на кривой.
Зная это, будет легче понять определение первого закона Кеплера, который гласит, что орбита планеты вокруг Солнца представляет собой эллипс, в одном из фокусов которого находится Солнце. Что ж, технически эллипсы и орбиты почти круглые, и это только усиливает представление о том, насколько удивительными были математические расчеты Кеплера и насколько точными были наблюдения Тихо.
Второй закон Кеплера гласит, что линия, проведенная от планеты к Солнцу, всегда проходит через равные площади за равные промежутки времени. Это так же легко понять, как и первый закон, несмотря на то, что звучит довольно сложно. Взгляните на схему на экране.
Третий закон Кеплера гласит, что квадрат периода обращения планеты пропорционален кубу ее большой полуоси.
Период обращения – это время, за которое планета совершает один оборот вокруг Солнца.
Большая полуось равна среднему расстоянию планеты от Солнца.
Взгляните на уравнение, представляющее третий закон Кеплера на экране. Буква «P» означает период обращения в «y» лет. Маленькая буква «а» обозначает большую полуось орбиты планеты, которая измеряется в а.е. или астрономических единицах.
Резюме
- Математика большинству людей не доставляет удовольствия, так что мы тут же прервем урок!
- Иоганн Кеплер был немецким астрономом и математиком, который думал, что он не очень хорош в математике или астрономии, но стал астрономом-революционером и блестящим математиком.
- Используя проницательные наблюдения, собранные астрономом Тихо Браге, и свои исключительные математические способности, Кеплер вывел три закона движения планет.
- Первый закон Кеплера гласит, что орбита планеты вокруг Солнца представляет собой эллипс, в одном из фокусов которого находится Солнце. Эллипс — это кривая, окружающая две точки, называемые фокусами, так что общее расстояние от одного фокуса до точки на эллипсе и обратно до другого фокуса постоянно для каждой точки на кривой. Второй закон Кеплера гласит, что линия, проведенная от планеты к Солнцу, всегда проходит через равные площади за равные промежутки времени.
- Третий закон Кеплера гласит, что квадрат периода обращения планеты пропорционален кубу ее большой полуоси.
- Период обращения — это время, за которое планета совершает один оборот вокруг Солнца, а большая полуось равна среднему расстоянию планеты от Солнца.